Laser Power Calibration using Camera

based on camera specifications

The Equipment Setup

The setup is shown in the image below.

Shining a laser directly into the lens of a camera is probably a bad idea.

By scattering the laser beam and then taking advantage of the inverse square law, we can get any attenuation we want.

A Lambert surface scatters light in a predictable manner. Paper can make a good Lambertian surface. link We had some paper that matched the description of what was used in the link.

We imagine a hemisphere centered on the point at which the laser beam strikes the paper. If we know the radiant flux density (watts per square meter) on the surface of the sphere directly above the paper, we can predict what it should be anywhere else on the surface of the hemisphere.
E' = E cosθ
Where:
E is the radiant flux density on the surface of the hemisphere
   exactly above the middle of our Lambertian surface.
E' is the radiant flux density at the camera lens.
θ is the angle between the reference point and the camera lens
The process will go as follows:

Calculate the Power Received by the Camera

The camera was set up such that a picture could be taken of the scattered laser light without saturating.

The aperture was left wide open. The analog gain was set to unity. The exposure time was 1/1000 second.

Full Well Capacity (FWC) = 8180 #taken from Strolls with my Dog

The data from the camera was surprising so a total of four images was taken with the paper being rotated between each image.

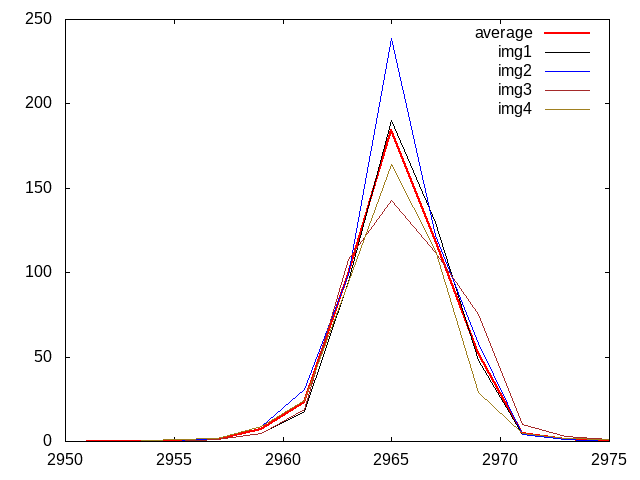
The surprise is how much the energy seems to be concentrated in the middle of the laser beam.

Based on an initial guess about the width of the laser beam, the statistical calculations were based on 1 mm cubes.

With the equipment set up as it is, 1 mm at the center of the graduated cylinder is about 14 pixels at the camera.
fwc = 8180. #full well capacity
mdn = 255. #max digital number

f = open("ave.txt", 'r')

total = 0
l = f.readline()
while l != "":
    pos = l.find(" ")
    num = int(l[pos:])
    total = total + num
    l = f.readline()

#that's for an array 15 x 1
#to get a 1 mm square area multiply by 206/15

total = total * 206./15.


f.close()
print(total)
#the red pixels are 1/4 of the total pixels
#to get the correct energy landing on the 1 mm square,
#multiply the electrons by four

electrons = 4 * int(fwc * total / mdn)
print("electrons", electrons)

h = 6.6e-34
c = 3e8

lmbda = 640e-9

ee = h*c/lmbda #electron energy (joules)
print("electron energy", ee, "joules")
eas = electrons * ee #energy at sensor (joules) per 1 mm square
print("energy at sensor", eas, "joules")
The result is:
6743.066666666667
electrons 865228
electron energy 3.09375e-19 joules
energy at sensor 2.676799125e-13 joules

How does the Power at the Reference Point Relate to the Laser Power?

A numerical model was constructed for the hemisphere. The reference point was taken as 1 unit and the power illuminating the surface of the hemisphere was calculated. That provides a ratio between the reference point power and the laser power.

The hemisphere was modeled as a stack of rings of varying radius. The inner surface of each ring was 1 mm wide so the inner surface area of each ring would be 1 mm x 2 * pi * r where r is in mm.

The total power illuminating each ring would be the ring area x cosθ. In the following code, angle α was used to calcualte each ring radius so the power illuminating the ring would be cos(90° - α).
#a set of stacked rings approximating a hemisphere
#the power flux at the top of the hemisphere is set to 1

from math import pi
from math import cos
from math import acos
from math import sin
from math import asin

pMax = 1.
r = 300. #mm
arcLen = pi*r/2. #quarter circle arc length
arcAng = pi/2 #radians in quarter circle
inc = 1. #1 mm approximate square
incAng = arcAng * inc / arcLen

totalPwr = 0
ringAng = incAng/2
while ringAng < arcAng:
    ringRadius = r - (r * sin(ringAng))
    print(ringAng, ringRadius)
    ringCirc = 2*pi*ringRadius
    ringPwr = inc * ringCirc * cos(arcAng - ringAng)
    totalPwr = totalPwr + ringPwr
    ringAng = ringAng + incAng
print("total power", totalPwr)
The result was:
total power 121354.7
So, if we multiply the power illuminating the reference point by the ratio, rat = 121355, we get the total power illuminating the inside surface of the hemisphere.

Laser Power Calculation

In the diagram above the hypotenuse, h = 300 mm.
The base, b = 280 mm.
The angle α = 0.367 radians = 21°
The angle θ = π/2 - α = 1.2 radians = 69°
From above, energy at sensor, es = 2.676799125e-13 joules
The energy at the reference point, er = es x cos(69°)
The reflectance of the paper was taken as, refl = 0.8
The laser energy, le = er x rat / refl = 1.13e-7 joules
The exposure time was et = 0.001 second.
The laser power was, lp = le / et = 0.11 mw.