Statistical Analysis

This analysis assumes that a photon undergoes one, and only one collision between the laser and the camera. It seems to work for our diluted coffee solutions (40 ml coffee in 160 ml distilled water). (I hasten to add that multiple collisions happen. This analysis doesn't cover them. There is a note at the bottom of the page about how to recognize the two situations.)

We divide the path of the laser beam into 1mm cubes.

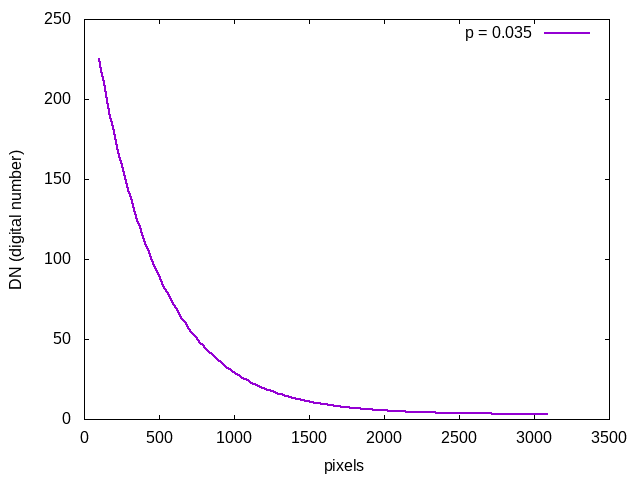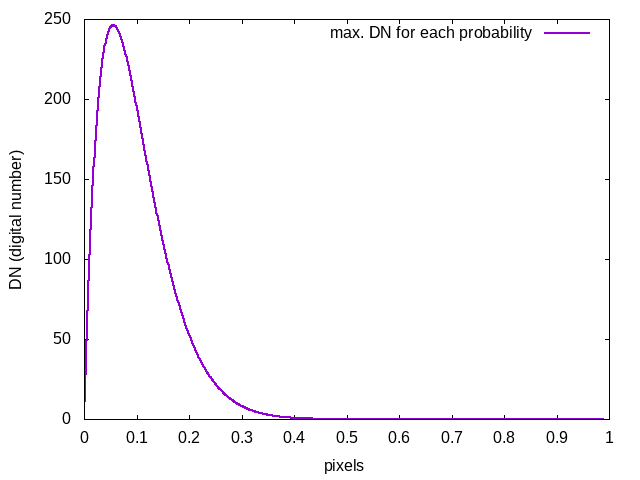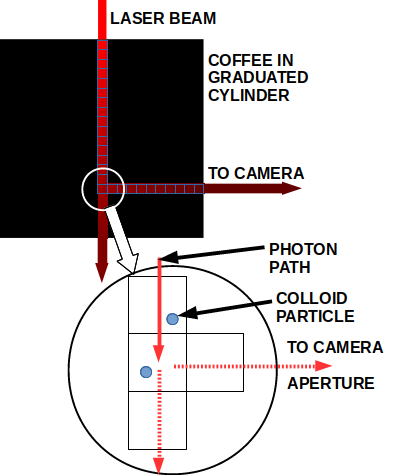
There is a probability, p, that a photon will encounter a colloid particle and be reflected in some other direction.

Thus, the probability that the photon will make it to the next cube in line is 1 - p.

The probability that a photon will make it through a line of n cubes is (1-p)n

We will assume that a photon colliding with a colloid particle can be reflected in any direction, ie. that the collision is an omnidirectional radiator. (That is at odds with how light scattering in colloidal dispersions is conventionally described, especially for small particle sizes. Unless I've made an error, it seems to work as a first approximation. It doesn't work for a detailed calculation of signal strength. For that, you have to use MIE scattering.)

The probability that the photon will be refleted toward the aperture of the camera is small. It's a function of the area of the aperture and the distance between the camera and the reflecting colloid particle. It will be treated as a constant and ignored for the time being.

Normalizing the Probabilities

We can graph the signal received at the camera from each point along the laser beam.
Note that each probability has a maximum value. In this case it is around 225.

The camera is set up such that the maximum value for a red pixel is 255. So, we don't want the maximum single reflection signal to exceed that. We can plot the maximum value for each probability against its p value.
We find a maximum DN of 246 for p = 0.056. We normalize the various probability curves such that their maxima lie on this curve.

Does the Posited Theory Match the Measured Data?

The sample was 40 ml of coffee made in the MoccaMaster diluted with 160 ml of distilled water.

A laser was shone down the middle of a graduated cylinder containing the sample. A picture was taken of the light scattered from the laser beam. The camera was a Raspberry Pi High Quality camera. The image format was RAW. Digital numbers (DN) representing the red pixels along the laser beam were extracted to a plot file.

The left image is a graph of the digital numbers vs. their position (measured in pixels) along the laser beam. Note that the signal has a baseline noise of about 15 DN.

The middle image is the left image with a plot of the curve for p = 0.035.

The right image has the two curves shifted. The measured data curve is shifted down to remove the effect of the baseline noise. The calculated curve is shifted right to remove the effect of the camera's alignment.

In a subsequent page I will show that the p value is a function of the colloid concentration and the particle size.

Multiple Collisions

Multiple collisions can be detected by examining the picture of the illuminated sample. If any light shows away from the direct laser beam, it can only have been created as a result of more than one collision.